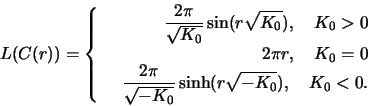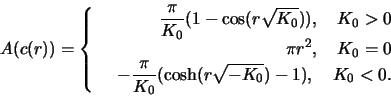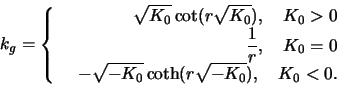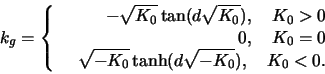DIFFERENTIAL GEOMETRY MN1 FALL 2001
PROBLEMS
- 6.
- Let
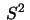 be the sphere
be the sphere
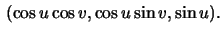 Let
Let
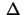 be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle
be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle  Show that
Show that
In which direction has the vector turned when it returns to its
original position? What is the area of the spherical surface bounded
by the latitude circle on the upper
half sphere?
- 7.
- The surface of revolution
is generated by revolving the curve 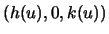 about the
about the 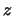 -axis.
We assume that
-axis.
We assume that
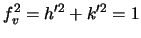 and hence that
and hence that 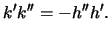 Prove that
Prove that
Use these results to prove that the Gauss curvature
The requirement that f has constant Gauss curvature 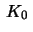 means
that
means
that 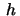 must satisfy
must satisfy
Conversely, a function 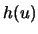 satisfying
satisfying 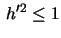 will enable us
to construct interesting surfaces of constant Gauss curvature
will enable us
to construct interesting surfaces of constant Gauss curvature 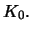
Consider the surface of revolution with
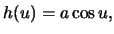 where
where 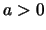 and
and
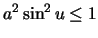 , which implies
that
, which implies
that
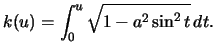 Prove that this surface has constant Gauss curvature
Prove that this surface has constant Gauss curvature 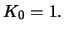 For what values of
For what values of 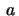 is the surface
a sphere?
Answer:
is the surface
a sphere?
Answer: 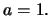
If we let
we obtain a surface of revolution with 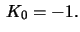 The curve
generating the surface is a tractrix and the surface is called
s pseudosphere.
The curve
generating the surface is a tractrix and the surface is called
s pseudosphere.
- 8.
- Let
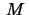 be a Riemann surface with constant Gauss curvature
be a Riemann surface with constant Gauss curvature 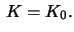
- a)
- Calculate the circumference and area of a circle with radius
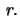
- b)
- Calculate the geodesic curvature
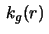 of a circle with
radius
of a circle with
radius
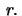 Determine
Determine
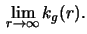
- c)
- Let
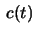 be a geodesic
and
be a geodesic
and
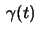 a curve whose distance to
a curve whose distance to
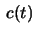 is constant
is constant 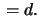 Calculate the geodesic curvature
Calculate the geodesic curvature
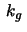 of the equidistant curve
of the equidistant curve 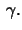
RESULTS
WARNING! THERE ARE VERY LIKELY MISPRINTS HERE!
a)
b)
c)
Back
to Differential Geometry MN1 Fall 2001


![]() where
where ![]() and
and
![]() , which implies
that
, which implies
that
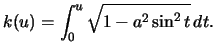 Prove that this surface has constant Gauss curvature
Prove that this surface has constant Gauss curvature ![]() For what values of
For what values of ![]() is the surface
a sphere?
Answer:
is the surface
a sphere?
Answer: ![]()