$\parbox{0.45\textwidth}{\begin{flushleft}\vspace{-\baselineskip} {\L... ...tet}\\ \textbf{Matematiska Institutionen}\\ Thomas Erlandsson \end{flushleft}}$

DIFFERENTIAL GEOMETRY MN1 FALL 2001

PROBLEMS

9.

Let $\,f:(a,b)\times (c,d)\to R^3\,$ be a surface in $R^3\,$ with constant Gauss curvature $\,K<0,$ defined in asymptotic coordinates, and parametrized by arc length so that

$$\,g_{11}(u)=g_{22}(u)=1.$$

Let $\,\omega(u_0^1,u_0^2)\,$ be the unique number $\,0<\omega(u_0^1,u_0^2)<\pi\,$ such that $\,\omega(u_0^1,u_0^2)\,$ is the angle between $\,f_{u^1}(u^1,u_0^2)\vert _{u^1=u_0^1}\,$ and $\,f_{u^2}(u_0^1,u^2)\vert _{u^2=u_0^2},$ i.e.

$$\,g_{12}(u)=\cos \omega(u).$$

a) Show that $\,\omega\,$ satisfies the differential equation

$$\frac{\partial^2\omega}{\partial u^1 \partial u^2}=(-K)\sin\omega$$

Hint: Use Gauss' equation which in the coordinates of the problem is

$$K = \frac{1}{2\sqrt{1-(g_{12})^2}}\left[ \frac{\partial}{\par... ...^2}}\left ( \frac{g_{12,1}}{\sqrt{1-(g_{12})^2}}\right)\right]$$

b) Show that every polygon $\,Q\,$ with four sides and which is bounded by parameter curves has the area

$$\frac{1}{-K}\left(\sum_{i=1}^4\alpha_{i}-2\pi\right)\le\frac{2\pi}{-K},$$

where $\,\alpha_{i}\,$ are the inner angles in $\,Q.$

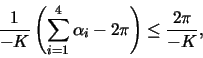
Hint: The area element is $\sqrt{g_{11}g_{22}-(g_{12})^2}=\sin\omega\, du^1 du^2.$

10.

(For VG only)

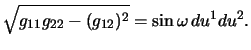
The Poincaré Upper Half Plane Model of $\,H^2$

The surface $\,H^2\,$ is in the Poincaré upper half plane model the set

$$\,U=\{(u,v) \in R^2\vert\,v >0\}\,$$

with the Riemann metric

$$\,ds^2= \frac{du^2+dv^2}{v^2}.$$

Using Gauss' equation we find immediately that this surface has constant Gauss curvature
$\,K=-1.$ The line element $\,ds^2\,$ in $\,H^2\,$ is equal to the euclidean line element $\,du^2+dv^2\,$ multiplied by a strictly positive function. Therefore an angle measured with respect to the Riemann metric coincides with the euclidean angle.

The geodesics in the upper half plane model of $\,H^2\,$ are the euclidean circles and straight lines which meet the boundary $\,v=0\,$ orthogonally. This can be shown in the following way:

In $\,H^2\,$ we get $\,g_{11}=1/v^2,\quad g_{12}=0,\quad g_{22}=1/v^2$ and it follows that

$$\,\Gamma^{1}_{11}=\Gamma^{1}_{22}= \Gamma^{2}_{12}= 0,\quad\Gamma^{2}_{11}= -\Gamma^{2}_{22}= -\Gamma^{1}_{21}=1/v.$$

The differential equations of the geodesics can therefore be written

$$\ddot u-\frac{2\dot u \dot v }{v}=0,\quad \ddot v+\frac{{\dot u}^2 -{\dot v }^2}{v}=0.$$

If $\,\dot u =0\,$ then $\,u=$ constant. In this case it is clear that the geodesic is a straight euclidean line orthogonal to $\,v=0.$

If $\,\dot u \ne 0\,$ we get from the first equation that $\ln(\dot u/v^2)\,=$ constant so $\,\dot u = cv^2\ne 0\,$ for some constant $\,c.$ In the same way we get from the second equation that $\,{\dot u}^2+{\dot v}^2=bv^2 >0\,$ for some constant $\,b.$ By combining these equations we get $\,(dv/du)^2={\dot v}^2/{\dot u}^2 =b/c^2v^2-1.$ Therefore $\,(u-a)^2+v^2=b/c^2\,$ for some constant $\,a.$ This is a circle with centre on $\,v=0$ and so meets $\,v=0\,$ orthogonally.

The isometries of $H^2$ are well-known maps in the upper half plane model. Let $\,SL(2, R)\,$ be the special linear group in dimension 2, i.e. the group of all real $\,(2\times 2)$-matrices with determinant $\,=1.$ $\,SL(2, R)\,$ acts on $\,H^2\,$ in the following way. Let $\,z=u+iv.$ The points $\,(u,v)\,$ in the upper half plane correspond to $\,z=u+iv,\,\,\,v>0.$ If

$$g = \left(\begin{array}{rrrr} a&b\\ c&d\end{array}\right)\in SL(2, R),$$

let

$$gz=\frac{az+b}{cz+d}.$$

Proposition

The group $\,SL(2, R)\,$ acts as a group of isometries on $\,H^2.$

Proof: Let $\,u+iv=z\,$ and

$$\,\frac{az+b}{cz+d}=\tilde z.$$

If we write $\,dz\,d\bar z\,$ for $\,du^2+dv^2\,$ the line element of $\,H^2\,$ can be written

$$ds^2(z)=\frac{-4dz\,d\bar z}{(z-\bar z)^2}, \qquad \bar z=u-iv.$$

As $\,d\tilde z=d((az+b)(cz+d))=dz/((cz+d)^2\,$ it follows that $\,ds^2(z)=ds^2(\tilde z),$ which means that $\,z\mapsto\tilde z\,$ is an isometry.

a)

Calculate the arc length of the geodesic $\,c(t)=(r\cos t, r\sin t),\,\,0 < t < \pi\,$ starting from the top of the half circle , $\,t=\pi/2.$ $\qquad$ (Result: $\vert\ln \tan \frac{t}{2}\vert$)

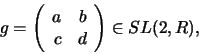
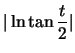Calculate also the arc length of the geodesic $\,u=u_0\,$ from $\,v=a\,$ till $\,v=b.$
(Result: $(\vert\ln \frac{a}{b}\vert$)

b)

Calculate the geodesic curvature $\,k_{g}\,$ of the curve $\,v=1.$ $\quad$ (Result: $\,k_{g}=1$)

The Poincaré Disc Model

The surface $\,H^2\,$ in the Poincaré disc model is the set

$$U=\{(u,v) \in R^2\vert u^2+ v^2 < 4\},$$

with the Riemann metric

$$\,ds^2=\left(1-\frac{u^2 + v^2}{4}\right)^{-2} (du^2+dv^2).$$

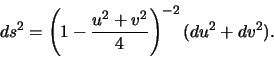
Using Gauss' equation we find that the surface has constant Gauss curvature $\,K=-1.$ The geodesics in the disc model correspond to the circles orthogonal to the boundary of the disc and the diameters. This is most easily seen by showing that the map

$$w=\frac{z+2i}{iz+2}$$

is an isometry of the disc model onto the half plane model.

d)

Calculate the arc length $\,r\,$ of the geodesic $\,c(t)=(t\cos \vartheta, t\sin \vartheta),\,\,0 \le t < 2\,$ beginning at origo.

$\quad$ (Result: $r=\ln\frac{2+t}{2-t}=2 \frac{1}{2}\ln\frac{1+t/2}{1-t/2}= 2\tanh^{-1}(t/2)$)

e)

Show that in geodesic polar coordinates

$$ds^2 = dr^2+\sinh ^{2}(r)\, d\theta^2.$$

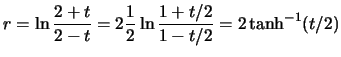Hint: From the problem above follows that $\,t = 2\tanh (r/2).$
Use $\,u=t\cos\theta, v=t\sin\theta\,$ and the given metric.

Back to Differential Geometry MN1 Fall 2001