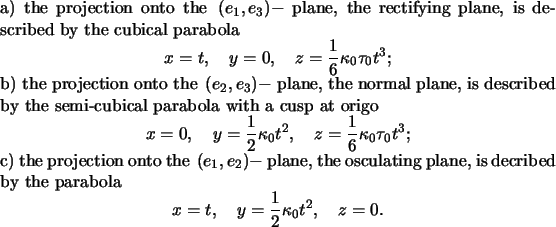DIFFERENTIAL GEOMETRY MN1 FALL 1999
PROBLEM 1-5
1. Show that the curvature of a plane curve is in general given by
the formula
2. Show that the curvature and torsion of a space curve are in
general given by the formulae
where
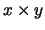 is the vector product in R3.
is the vector product in R3.
3. Let 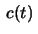 be a
curve in
be a
curve in 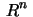 parametrized by arc length
with the property that
parametrized by arc length
with the property that
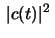 has a local maximum
at
has a local maximum
at 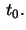 Let
Let
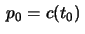 and
and
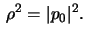 Show that
Show that
where
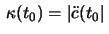 (which is equal to the first curvature of
(which is equal to the first curvature of 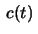 at
at 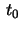 if it is
defined).
if it is
defined).
4. Let
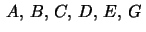 be constants such that
be constants such that
Consider the curves
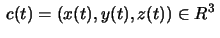 whose
tangent vectors at each point
whose
tangent vectors at each point
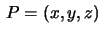 in space are in the plane
in space are in the plane 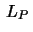 through
through
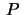 whose
normal
is
whose
normal
is
(Bz-Cy+D,Cx-Az+E,Ay-Bx+G).
It is clear that such curves satisfy
Let 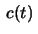 be a curve which satisfies such a condition
and assume that
be a curve which satisfies such a condition
and assume that
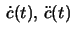 are linearly independent at
are linearly independent at 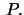 Let
Let
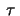 be the torsion of the curve at
be the torsion of the curve at
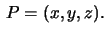
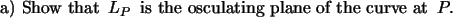
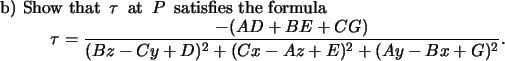
5. Let 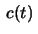 be a curve
in
be a curve
in 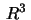 parametrized by arc length
and let
parametrized by arc length
and let
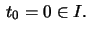 Let the Frenet-frame at
Let the Frenet-frame at 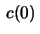 be
be
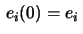 and let
and let
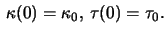 We then have the following well known series expansion for
We then have the following well known series expansion for 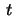 close to
close to 
The projections of the curve in a small neighbourhood of 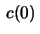 in
the planes
of the Frenet-frame at that point are therefore approximated by the
following curves:
in
the planes
of the Frenet-frame at that point are therefore approximated by the
following curves:
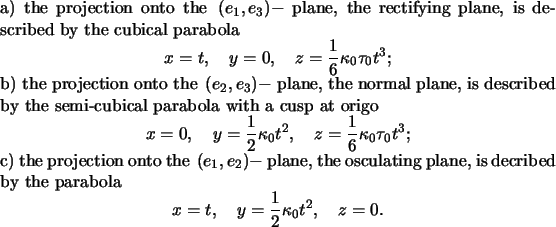

Tillbaka
till Differentialgeometri MN1


![]() be a
curve in
be a
curve in ![]() parametrized by arc length
with the property that
parametrized by arc length
with the property that
![]() has a local maximum
at
has a local maximum
at ![]() Let
Let
![]() and
and
![]() Show that
Show that
![]() be constants such that
be constants such that ![]()
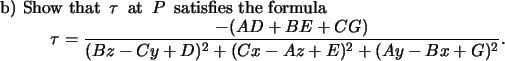
![]() be a curve
in
be a curve
in ![]() parametrized by arc length
and let
parametrized by arc length
and let
![]() Let the Frenet-frame at
Let the Frenet-frame at ![]() be
be
![]() and let
and let
![]() We then have the following well known series expansion for
We then have the following well known series expansion for ![]() close to
close to ![]()