FÖRDJUPNINGSAVSNITT FÖR NVP-PROGRAMMET
Ch 2.7 APPLICATIONS TO COMPUTER GRAPHICS
Här introduceras en genial uppfinning,
homogena
koordinater, som ofta betecknas
![$\,[x,y,z],$](img3.gif)
där minst ett av talen
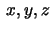
är
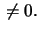
Då svarar
![$\,[x,y,z],$](img3.gif)
och
![$\,[\lambda x,\lambda
y,\lambda z], \,\,\lambda\ne 0$](img6.gif)
mot samma punkt. Punkterna
![$\,[x,y,1]\,$](img7.gif)
svarar en-entydigt
mot punkterna i
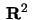
och punkterna
![$\,[x,1,0]\,$](img9.gif)
och
![$\,[1,0,0]\,$](img10.gif)
mot punkterna i
oändligheten. Alla dessa punkter
kan representeras i ett ändligt plan, det s k
projektiva
planet. Om vi använder homogena koordinater kan även
translationer beräknas genom att multiplicera matriser vilket visas i
Exempel 4.
Övningar: 1, 3, 5, 7, 11, 13, 15, 17, 19
Inlämningsuppgifter: 18, 20
Ch 7.4 THE SINGULAR VALUE DECOMPOSITION
En
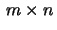
matris
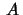
svarar mot en linjär transformation
från
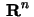
till
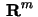
och
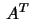
svarar
mot en linjär transformation från
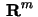
till
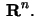
Detta innebär att matrisen
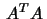
svarar mot en symmetrisk linjär
operator på
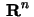
som alltså är ortogonalt
diagonaliserbar med icke-negativa egenvärden
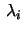
(s. 473) oavsett om
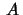
är diagonaliserbar eller ens kvadratisk.
Talen
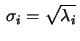
är de
singulära värdena av 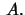
Genom en
singular value decomposition kan man t ex få fina
baser för de fundamentala delrummen av
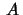
som visas i
Exempel 6.
Övningar: 1, 3, 5, 7, 9, 15, 23
Inlämningsuppgift: 13
BONUSPOÄNG FÖR NVP-PROGRAMMET
- 1.
- Korrekta handskrivna lösningar av de tre inlämningsuppgifterna som
lämnas in
senast måndag 10/3
ger 1 bonuspoäng. Därefter är det försent att lämna in
lösningar. Godkänd tentamen den 17/3 räcker dock för att bli godkänd på
kursen utan att man lämnat in dessa uppgifter.
- 2.
- På tentamen den 17/3 kommer efter de ordinarie problemen två
extra problem, ett på Ch 2.7 och ett på Ch 7.4, som kommer att vara av
samma typ som de föreslagna övningarna och
inlämningsuppgifterna. Korrekta lösningar av dessa problem ger 1
bonuspoäng per problem. Dessa poäng kan man få även om man inte har
lämnat in lösningar på inlämningsuppgifterna.
Tillbaka till Linjär algebra MN1



