lasanv602

$\textstyle \parbox{0.45\textwidth}{\begin{flushleft}\vspace{-\baselineskip} {\L... ...itet}\\ \textbf{Matematiska Institutionen}\\ T Erlandsson\\ \end{flushleft}}$ $\textstyle \parbox{0.45\textwidth}{\begin{flushright}\vspace{-\baselineskip} \par LINJÄR ALGEBRA MN1\\ LÄSANVISNINGAR\\ CHAPTER 6\end{flushright}}$

SECTION 6.1

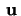
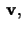
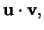
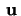
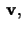
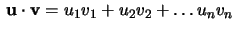
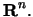
The inner product of $\,\mathbf{u}\,$ and $\,\mathbf{v},$ som ofta betecknas $\mathbf{u}\cdot\mathbf{v},$ kallas inre produkten eller skalärprodukten av $\,\mathbf{u}\,$ och $\,\mathbf{v},$ och i det fall att $\,\mathbf{u}\cdot\mathbf{v}=u_1v_1 + u_2v_2 +\dots u_nv_n\,$ talar vi om standardskalärprodukten på $\mathbf{R}^n.$ På engelska är det också naturligt att säga the standard inner product. Med hjälp av den inre produkten kan vi införa begreppen längd, ortogonalitet och vinkel i våra vektorrum, dvs vi kan nu geometrisera rummen.

Ledning Exercise 24: $\vert\vert\mathbf{u}\pm\mathbf{v}\vert\vert^2=(\mathbf{u}\pm\mathbf{v})\cdot(\mathbf{u}\pm\mathbf{v})$

SECTION 6.2

THEOREM 5 förklarar varför vi tycker om ortogonala baser. Avnittet
An Orthogonal Projection på sidan 380 är viktigt. Observera betydelsen av orthogonal matrix på sidan 385. En sådan har ortonormala kolonner och automatiskt, ortonormala rader.

THEOREM 9 THE BEST APPROXIMATION THEOREM visar att ortogonala projektioner måste vara exceptionellt viktiga inom vetenskapen.

Notera vad David Lay säger före EXEMPEL 2. ``Study it carefully.'' QR Factorization of Matrices är överkurs men helt oemotståndligt.

SECTION 6.7

Jag vet inget viktigare avsnitt än CH 6.7 Inner Product Spaces. Differentialgeometri, allmän relativitetsteori mm mm skulle ju inte finnas utan denna generalisering av inre produkt.