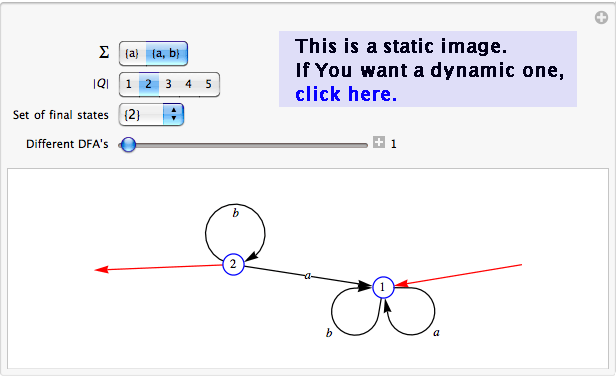
All DFA's with a given alphabet and a given set of states
How many are they?
A DFA's transition function δ is of type
where Q is the state set, and 
is the tape alphabet.
Thus δ has 
different pairs 
of inputs.
Why? Below follows an explanation.
δ is uniquely characterized by the choice of outputs in δ:s input-output table.
So the number of transition functions is the same as the number of such rows of outputs.
Well, how many different rows are there?
Let’s see ….
Such a row contains 
cells – one cell for every input pair 
.
As the outputs are chosen from Q, there are {Q} ways to fill each cell.
Considering a whole row, cell by cell, there must be 
different fillings. This explains (2). Now we know how many ways there are to design a transition function δ.
To construct a DFA with a certain transition function δ, let us always denote the initial state by 1, and other states by greater numbers. All we have to do to get a complete description of such a DFA is to decide which states should constitute the set of final states. As every subset of Q is a potential choice for this, and there are 
different subsets of Q, the number of possible choices for the set of final states is 
.
It follows that the total number of DFA's is
