- Consider the circular helix
Show that its curvature  and torsion
and torsion 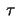 are given
by the formulae
Hint: Use the formulae in Exercise 1.6.3 in our paper
on curves.
are given
by the formulae
Hint: Use the formulae in Exercise 1.6.3 in our paper
on curves.
Note that if 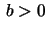 (so that
(so that 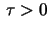 ) the helix is a
``right-handed'' curve and if
) the helix is a
``right-handed'' curve and if 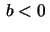
(so that  ) it is ``left-handed''. Draw a picture to illustrate
the meaning of right and left-handed. Be careful with the choice of
orientations of the curves. Prove that it is not possible to find an
isometry of
) it is ``left-handed''. Draw a picture to illustrate
the meaning of right and left-handed. Be careful with the choice of
orientations of the curves. Prove that it is not possible to find an
isometry of 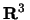 which maps a
right-handed helix onto a left-handed.
which maps a
right-handed helix onto a left-handed.
- Prove that a regular, nice curve
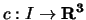 is a plane curve if and
only if its torsion vanishes identically.
is a plane curve if and
only if its torsion vanishes identically.
Hint: It is no restriction to assume the curve is
parameterized by arc-length. Let
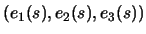 be the distinguished Frenet frame. Use the
Frenet equations to conclude that
be the distinguished Frenet frame. Use the
Frenet equations to conclude that
 a constant
vector, and from the fact that
a constant
vector, and from the fact that  and
and  are
orthogonal prove that
are
orthogonal prove that
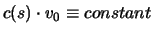 by integration.
by integration.
- Prove that a regular, nice curve
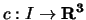 is a straight line if
is a straight line if 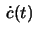 and
and 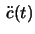 are linearly dependent
for all
are linearly dependent
for all 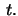
Hint: What is the torsion and the curvature of such a curve? We also need a
certain characterization of straight lines to be found in our paper on
curves.
- Find the most general function
 so that the curve
so that the curve
 will be a plane curve.
will be a plane curve.
Answer:
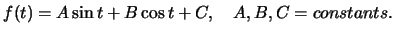
- Let
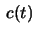 be a curve
in
be a curve
in 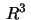 parametrized by arc length
and let
parametrized by arc length
and let 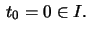 Let the Frenet-frame at
Let the Frenet-frame at 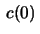 be
be
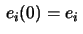 and let
and let
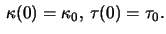 We then have the following well known series expansion for
We then have the following well known series expansion for 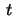 close to
close to 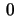
The projections of the curve in a small neighbourhood of 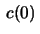 in
the planes
of the Frenet-frame at that point are therefore approximated by the
following curves:
in
the planes
of the Frenet-frame at that point are therefore approximated by the
following curves:
- a)
- the projection onto the
 plane, the rectifying
plane, is described by the cubical parabola
plane, the rectifying
plane, is described by the cubical parabola
- b)
- the projection onto the
 plane, the normal
plane, is described by the semi-cubical
parabola with a cusp at origo
plane, the normal
plane, is described by the semi-cubical
parabola with a cusp at origo
- c)
- the projection onto the
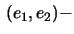 plane, the osculating
plane, is decribed by the parabola
plane, the osculating
plane, is decribed by the parabola
- i)
- Draw these projektions and their orientations
in the case
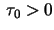 and
and 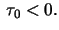
- ii)
- (For VG only) We shall now study what the curve looks like along the
negative
 axis
if we raise or lower our eyes somewhat above or under
the osculating plane. This means that we shall find
the projection of the curve in a
axis
if we raise or lower our eyes somewhat above or under
the osculating plane. This means that we shall find
the projection of the curve in a
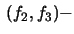 plane where the
plane where the  system
system
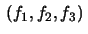 is created from the system
is created from the system
 by letting the
by letting the
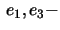 plane rotate a small angle
plane rotate a small angle
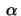
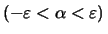 with
the
with
the 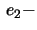 axis as axis of rotation.
Derive the analytical expression of the projection and draw
pictures of how it looks for different values of
axis as axis of rotation.
Derive the analytical expression of the projection and draw
pictures of how it looks for different values of  in the
cases
in the
cases 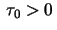 and
and 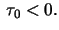



![]() (so that
(so that ![]() ) the helix is a
``right-handed'' curve and if
) the helix is a
``right-handed'' curve and if ![]()
![]() ) it is ``left-handed''. Draw a picture to illustrate
the meaning of right and left-handed. Be careful with the choice of
orientations of the curves. Prove that it is not possible to find an
isometry of
) it is ``left-handed''. Draw a picture to illustrate
the meaning of right and left-handed. Be careful with the choice of
orientations of the curves. Prove that it is not possible to find an
isometry of ![]() which maps a
right-handed helix onto a left-handed.
which maps a
right-handed helix onto a left-handed.
![]() be the distinguished Frenet frame. Use the
Frenet equations to conclude that
be the distinguished Frenet frame. Use the
Frenet equations to conclude that
![]() a constant
vector, and from the fact that
a constant
vector, and from the fact that ![]() and
and ![]() are
orthogonal prove that
are
orthogonal prove that
![]() by integration.
by integration.
![]()