$\parbox{0.45\textwidth}{\begin{flushleft}\vspace{-\baselineskip} {\L... ...tet}\\ \textbf{Matematiska Institutionen}\\ Thomas Erlandsson \end{flushleft}}$

DIFFERENTIAL GEOMETRY MN1 FALL 1999

PROBLEM 7 - 8

7. Assume that $\,f:U \to R^3\,$ is a surface whose principal curvatures $\kappa_1$ and $\kappa_2$ satisfy $\kappa_1\kappa_2\ne 0\,$ and $\kappa_1 \ne\kappa_2$ at all points in $\,U.$ Let $\,n\,$ be the unit normal and let $\,(u^1,u^2)\,$ be principal curvature coordinates. Show that the functions

$$b_i(u)=f(u)+n(u)/\kappa_i(u),\,\,i=1,2$$

are regular surfaces if and only if $\kappa_{1,1}\ne 0\,$ and $\,\kappa_{2,2}\ne 0.$ These surfaces are called the caustic surfaces of $\,f.$

8. Let $\,f:(a,b)\times (c,d)\to R^3\,$ be a surface in $R^3\,$ with constant Gauss curvature $\,K<0,$ defined in asymptotic coordinates, and parametrized by arc length so that

$$\,g_{11}(u)=g_{22}(u)=1.$$

Let $\,\omega(u_0^1,u_0^2)\,$ be the unique number $\,0<\omega(u_0^1,u_0^2)<\pi\,$ such that $\,\omega(u_0^1,u_0^2)\,$ is the angle between $\,f_{u^1}(u^1,u_0^2)\vert _{u^1=u_0^1}\,$ and $\,f_{u^2}(u_0^1,u^2)\vert _{u^2=u_0^2},$ i.e.

$$\,g_{12}(u)=\cos \omega(u).$$

a) Show that $\,\omega\,$ satisfies the differential equation

$$\frac{\partial^2\omega}{\partial u^1 \partial u^2}=(-K)\sin\omega$$

Hint: Use Gauss' equation which in the coordinates of the problem is

$$K = \frac{1}{2\sqrt{1-(g_{12})^2}}\left[ \frac{\partial}{\par... ...^2}}\left ( \frac{g_{12,1}}{\sqrt{1-(g_{12})^2}}\right)\right]$$

b) Show that every polygon $\,Q\,$ with four sides and which is bounded by parameter curves has the area

$$\frac{1}{-K}\left(\sum_{i=1}^4\alpha_{i}-2\pi\right)\le\frac{2\pi}{-K},$$

where $\,\alpha_{i}\,$ are the inner angles in $\,Q.$

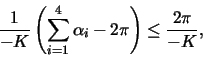
Hint: The area element is $\sqrt{g_{11}g_{22}-(g_{12})^2}=\sin\omega\, du^1 du^2.$

Tillbaka till Differentialgeometri MN1