DIFFERENTIAL GEOMETRY MN1 FALL 1999
PROBLEM 9 - 10
9. Let 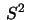 be the sphere
be the sphere
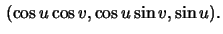 Let
Let
 be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle
be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle
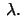 Show that
Show that
In which direction has the vector turned when it returns to its
original position? What is the area of the spherical surface bounded
by the latitude circle on the upper
half sphere?
10. When
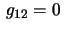 ,
i.e. in orthogonal coordinates, the
equations for
the geodesic lines are
,
i.e. in orthogonal coordinates, the
equations for
the geodesic lines are
In the case of a surface of rotation
the differential equation (2) of the geodesic lines is
One solution is
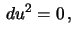 which shows that the meridians
are geodesic
lines. In all other cases the constant value of
which shows that the meridians
are geodesic
lines. In all other cases the constant value of
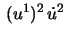 is denoted
is denoted 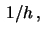 so that
so that
Show that
Hint:

Tillbaka
till Differentialgeometri MN1


![]() be the sphere
be the sphere
![]() Let
Let
![]() be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle
be the angle a vector has turned in relation to its
original position
after parallel translation of the vector around
the latitude circle with latitude angle
![]() Show that
Show that ![]() ,
i.e. in orthogonal coordinates, the
equations for
the geodesic lines are
,
i.e. in orthogonal coordinates, the
equations for
the geodesic lines are

![\begin{displaymath}u^2 = C \,\pm \, \int \left[\frac{1+{z_1}^2}{h^2(u^1)^2 -
1}\right]^{\frac{1}{2}}\,\frac{du^1}{u^1}.\end{displaymath}](img15.gif)
![]()