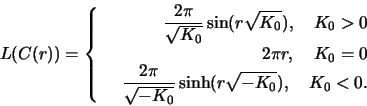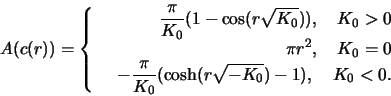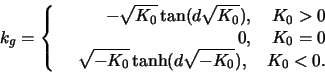DIFFERENTIAL GEOMETRY MN1 FALL 1999
PROBLEM 11
11. Let 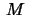 be a Riemann surface with constant Gauss curvature
be a Riemann surface with constant Gauss curvature
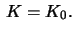
- a)
- Calculate the circumference and area of a circle with radius

- b)
- Calculate the geodesic curvature
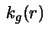 of a circle with
radius
of a circle with
radius
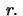 Determine
Determine
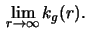
- c)
- Let
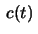 be a geodesic
and
be a geodesic
and
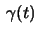 a curve whose distance to
a curve whose distance to
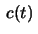 is constant
is constant 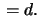 Calculate the geodesic curvature
Calculate the geodesic curvature
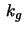 of the equidistant curve
of the equidistant curve 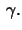
RESULTS
WARNING! THERE ARE VERY LIKELY MISPRINTS HERE!
a)
b)
c)
Tillbaka
till Differentialgeometri MN1


![]() be a Riemann surface with constant Gauss curvature
be a Riemann surface with constant Gauss curvature
![]()