DIFFERENTIAL GEOMETRY MN1 FALL 1999
PROBLEM 12 PAGE 2
The isometries of H2 are well-known maps in the upper half plane model.
Let
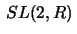 be the special linear group in dimension 2,
i.e. the group of all real
be the special linear group in dimension 2,
i.e. the group of all real
 -matrices with determinant
-matrices with determinant 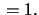
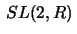 acts on
acts on 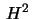 in the following way. Let
in the following way. Let
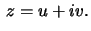 The points
The points 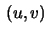 in the upper half plane correspond to
in the upper half plane correspond to
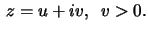 If
If
let
Proposition
The group
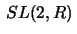 acts as a group of
isometries on
acts as a group of
isometries on
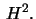
-
- Proof: Let
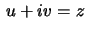 och
och
-
- If we write
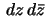 for
for
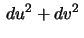 the line
element of
the line
element of
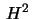 can be written
can be written
-
- As
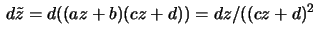 it follows that
it follows that
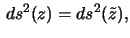 which means that
which means that
 is
an
isometry.
is
an
isometry.
- a)
- Calculate the arc length of the geodesic
 starting from the top of the half circle ,
starting from the top of the half circle ,
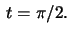
 (Result:
(Result:
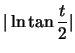 )
)
Calculate also the arc length
of the geodesic 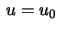 from
from 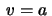 till
till 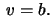
(Result:
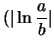 )
)
- b)
- Calculate the geodesic curvature
 of the curve
of the curve
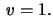
 (Result:
(Result:  )
)
- c)
- A vector is parallel translated the hyperbolic distance
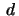 along the curve
along the curve 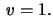 Calculate the angle the vector has turned during this translation.
Calculate the angle the vector has turned during this translation.
To
Problem 12 page 1
To
Problem 12 page 3
Tillbaka
till Differentialgeometri MN1


![]() be the special linear group in dimension 2,
i.e. the group of all real
be the special linear group in dimension 2,
i.e. the group of all real
![]() -matrices with determinant
-matrices with determinant ![]()
![]() acts on
acts on ![]() in the following way. Let
in the following way. Let
![]() The points
The points ![]() in the upper half plane correspond to
in the upper half plane correspond to
![]() If
If
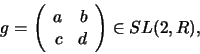
![]() acts as a group of
isometries on
acts as a group of
isometries on
![]()
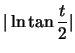 )
)
![]() from
from ![]() till
till ![]()
![]() )
)