

The surface ![]() in the Poincaré disc model is
the set
in the Poincaré disc model is
the set
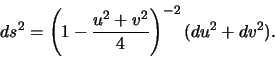
Using Gauss' equation we find that the surface has constant Gauss
curvature
![]() The geodesics in the disc model correspond to the circles orthogonal
to the boundary
of the disc and the diameters. This is most easily seen by showing
that the map
The geodesics in the disc model correspond to the circles orthogonal
to the boundary
of the disc and the diameters. This is most easily seen by showing
that the map
![]() (Result:
(Result:
 )
)
Hint: From the problem above follows that
![]()
Use
![]() and the given metric.
and the given metric.