

1. Let
![]() be
be
a)
![]()
b)

c)
![]()
d)
![]() 2. Let
2. Let
![]() be the torus
be the torus
a) ![]() is regular at each point
is regular at each point
b)
![]()
c)
![]()
d)
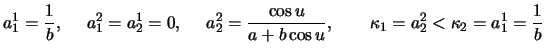
e)

Remark
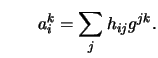
3. A surface
![]() defined by
defined by
![]() can be described as
can be described as
![]() Then
Then
a)


4.
![]() is a so called "monkey saddle".
It is a saddle used by a monkey riding a bicycle.
There are two depressions for its legs, and an extra one for its tail.
Show that the surface has a planar, umbilic point at origo,
i.e that
is a so called "monkey saddle".
It is a saddle used by a monkey riding a bicycle.
There are two depressions for its legs, and an extra one for its tail.
Show that the surface has a planar, umbilic point at origo,
i.e that ![]() at origo
and that the normal curvatures there are equal in all directions.
at origo
and that the normal curvatures there are equal in all directions.