

The axiomatic method in 2-dimensional geometry makes it possible to study a plane or a surface as an object in itself without an embedding in a surrounding space. The method has its limitations though, for example distances and areas are hard or even impossible to determine. In his famous paper 1827 on curved surfaces Gauss showed how to do geometric calculations in an efficient way in a surface without having to consider the surface as embedded in a surrounding space. This work became the foundation in 1854 for Riemann's theory of curved spaces, in which the geometry of the planes in a space are determined by the space itself.
To each point
![]() we associate a tangent plane
we associate a tangent plane
![]() which is a vector space isomorphic to
which is a vector space isomorphic to ![]() To obtain a basis in each such tangent plane
the basis
To obtain a basis in each such tangent plane
the basis
![]() in
in ![]() is translated parallel to itself
to
is translated parallel to itself
to ![]()
In every tangent plane
![]() where the point
where the point
![]() and
and
Such a set of scalar products is called a metric or
Riemannian metric or Riemann metric on ![]()
The form ![]() is a scalar product if
is a scalar product if
![]() for all
for all
![]() The functions
The functions
![]() och
och ![]() are assumed to be four times continuously
differentiable with respect to
are assumed to be four times continuously
differentiable with respect to
![]() och
och ![]() So the metric defines a positively definite bilinear form
So the metric defines a positively definite bilinear form ![]() on each tangent plane
on each tangent plane
![]() and is an example of a tensor.
In the literature a metric is often written in the form
and is an example of a tensor.
In the literature a metric is often written in the form
The expression (2) is to be interpreted as the bilinear form in (1).
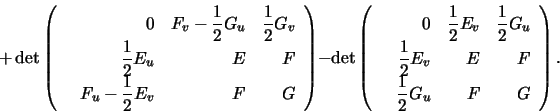
This expression, the Gauss equation, is complicated
but if ![]() the expression simplifies to
the expression simplifies to
![\begin{displaymath}K = -\frac{1}{\sqrt{\,EG}}\left[ \frac{\partial}{\partial
u}\...
...t{\,G}} \frac{\partial
\sqrt{\,E}}{\partial v}\right )
\right].\end{displaymath}](img29.gif)
When the Gauss curvature is constant it is possible to describe
the connection between the curvature and the geometry of the plane or surface
by
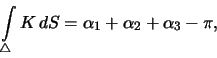
By using the metric we can in principle solve all geometric problems in
in a plane or a surface of Gaussian curvature ![]()
The straight lines, also called geodesics, are determined from a system of ordinary differential equations
So the solution curves of this system, which correspond to the straight lines in
the plane or the surface
whose Gaussian curvature is ![]() are curves in the open set
are curves in the open set
![]() in the euclidean plane in which we represent the geometry of the
plane or the surface.
in the euclidean plane in which we represent the geometry of the
plane or the surface.
The distance
![]() in the surface between two points
in the surface between two points ![]() and
and ![]() in
in ![]() corresponds to the arc length of the straight line,
i.e. the geodesic,
between
corresponds to the arc length of the straight line,
i.e. the geodesic,
between ![]() and
and ![]() in
in ![]() This distance is determined by the
metric and
is obtained from the line integral
This distance is determined by the
metric and
is obtained from the line integral
![\begin{displaymath}d(P,Q)=\int_P^Q \left[E\left(\frac{du}{ds}\right)^2+2F\frac{d...
...c{dv}{ds}
+G \left(\frac{dv}{ds}\right)^2\right]^{\frac{1}{2}}.\end{displaymath}](img42.gif)
Of course it is not the euclidean distance between ![]() and
and
![]() measured
with the standard scalarproduct in
measured
with the standard scalarproduct in ![]() which is the distance between
which is the distance between
![]() and
and
![]() in the surface.
in the surface.
The area of a geometric figure in a plane or a surface is obtained from the
integral

If
it follows from the Gauss equation that ![]() i.e.
the geometry is spherical. The area of the sphere is
i.e.
the geometry is spherical. The area of the sphere is
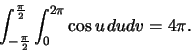
The curvature ![]() of a curve
of a curve
![]() in a plane or a
surface,
the so called geodesic curvature, is given by
in a plane or a
surface,
the so called geodesic curvature, is given by
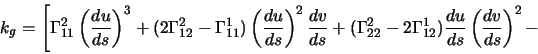
![\begin{displaymath}\left.-\Gamma^1_{22}\left(\frac{dv}{ds}\right)^3+\frac{du}{ds...
...^2v}{ds^2}-
\frac{d^2u}{ds^2}\frac{dv}{ds}\right]\sqrt{EG-F^2}.\end{displaymath}](img52.gif)
Along the curves
![]() and
and
![]() we get
the simpler
expressions
we get
the simpler
expressions
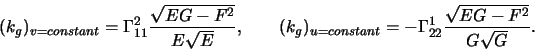
In case ![]() we get the even more simpler expressions
we get the even more simpler expressions
An important class of metrics are those which are proportional to the
standard
scalar product in each
![]() i.e.
i.e.
They can also be written on the form
Metrics of the type (3), (3') are called conformal. The euclidean angle
measured between two
vectors at ![]() with the standard scalar product in
with the standard scalar product in
![]() is then the same as the angle between the vectors
in the plane or surface
whose geometry we study if we use a metric like (3), (3').
is then the same as the angle between the vectors
in the plane or surface
whose geometry we study if we use a metric like (3), (3').
An open subset
![]() together with a metric
together with a metric ![]() is often called a model of the corresponding geometry. The italian
mathematician
Beltrami found in 1868 a number of suitable models for hyperbolic geometry
by using the theories of Gauss and Riemann.
These models were later used by
Poincaré and Klein in important works and therefore carry their names
instead.
is often called a model of the corresponding geometry. The italian
mathematician
Beltrami found in 1868 a number of suitable models for hyperbolic geometry
by using the theories of Gauss and Riemann.
These models were later used by
Poincaré and Klein in important works and therefore carry their names
instead.
The Gauss equation gives ![]() The model is conformal
so angles are determined directly in
The model is conformal
so angles are determined directly in ![]() The straight lines are all euclidean circles
and euclidean straight lines in
The straight lines are all euclidean circles
and euclidean straight lines in ![]() which are orthogonal to
which are orthogonal to ![]()
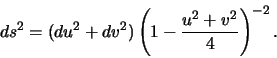
In this model ![]() and it is also conformal.
The straight lines are all diameters and all circles orthogonal to
and it is also conformal.
The straight lines are all diameters and all circles orthogonal to
![]()
There are simple formulas for distances in the conformal models. Define the double ratio
where ![]() denotes the euclidean distance between
denotes the euclidean distance between ![]() and
and ![]() etc.
etc.
PROP 1 The distance between two points ![]() and
and ![]() is in the
conformal models
is in the
conformal models
![]() and
and ![]() given by the formula
given by the formula
In this model ![]() and constant but the model is not conformal.
The straight lines correspond to
all euclidean chords in
and constant but the model is not conformal.
The straight lines correspond to
all euclidean chords in
![]() including all diameters.
Even if the model is not conformal
the euclidean angle between two diameters is in fact also the angle in the
hyperbolic plane. A chord which can be extended through the pole of
another chord cuts this chord under right angles in the hyperbolic plane.
including all diameters.
Even if the model is not conformal
the euclidean angle between two diameters is in fact also the angle in the
hyperbolic plane. A chord which can be extended through the pole of
another chord cuts this chord under right angles in the hyperbolic plane.
PROP 2 The distance between two points ![]() and
and ![]() is in the
Klein model
is in the
Klein model
![]() obtained from the formula
obtained from the formula