ETT EXTREMPROBLEM
                                            
Geometri D Ht 2000

                                                     

Kalle Ekström

                                         

I vissa webbläsare kan det hända märkliga saker med denna HTML-version, t ex är det inte säkert att bokstäverna i figurerna hamnar på rätt plats, så läsaren måste själv tänka efter var de ska vara.

Uppgift nr 75 kapitel 9 i Greenberg

 

Problem

Givet  en linje l och två punkter A och B som ligger på samma sida av linjen l och ett positivt tal  .

Bestäm i euklidisk geometri en linje mellan punkterna X och Y av längd d på l så att sträckan AXYB blir så kort som möjligt.

 

 

 

 

                                                                                                                        

                                                                                                                            B

                                                                                                                           

 

                             A                A’

                                                                                                    

 

          l

                                                  D        P      C            Q                                       O

                                                                  

 

 

 


                                                                                                                               B’

 

 

 

 

 

Lösning Reflektera punkten B över linjen l till punkten B’. Drag en linje parallell med l och med längd d från punkten A till punkten A’. Sammanbind punkterna A´ och B´ med en linje som skär linjen l i punkten C. Drag en  linje mellan punkterna B och C. 

Enligt S-V-S så är  och därför .

Drag från punkten A en linje parallell med linjen A’B’ till punkten D på linjen l.

Eftersom  och  så är . Det gäller också att  enligt S-V-S. Eftersom AD är parallell med A’C så är.

Då är sträckan  mellan punkterna A, D, C och B den kortaste sträckan .

 

För att visa att det är den kortaste sträckan så tar man två andra punkter med avståndet d på l och visar att den sträckan är längre än ADCB.

 

Bevis Tag två punkter Q,P på l   med avståndet d.

Låt vara sträckan mellan punkterna A och D.

Det som skall visas är att

                                         +.

Men    så det räcker med att visa att

                            

 Det gäller också att  eftersom På samma sätt är .Eftersom  så äroch på samma sätt är +.

Detta ger att + och

                                .

Eftersom    + ligger på en rät linje så är

                                  +   +.        

Vilket ger att

                                            

Alltså är

                                 

Som är det samma som

                                 

                                                                                    vsv.

Vad händer om punkterna A och B inte ligger på samma sida av linjen l ?

Problem

I den euklidiska geometrin är det givet  en linje l och två punkter A och B som inte ligger på samma sida av linjen l och ett positivt tal  .

Bestäm en linje mellan punkterna X och Y av längd d på l så att sträckan AXYB blir så kort som möjligt.

 

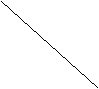
                                 A                A´

 

 

 

 

              l   

                                                           P    Q      P´        Q´

 

 

 

 

 

                                                                                                                  B

 

Lösning: Drag från punkten A en linje av längd d till punkten A’. Drag från punkten A’  en linje till punkten B.

Punkten P’ där  skär linjen l är en av de sökta punkterna.

Den andra punkten får man då man drar en linje från A parallell med linjen A´P´ till punkten P på l .

Då är  den kortaste vägen mellan punkterna A och B.

Bevis Tag två andra punkter Q och Q´på l.

Man skall visa att +.

.

 

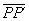
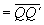
Eftersom  så räcker det med att visa att +.

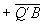
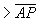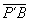Det gäller också att  eftersom  enligt S-V-S.

På samma sätt ges att  .

Då ger detta olikheten  vilken är sann eftersom punkterna A´, P´ och B´ ligger på en rät linje.

Alltså gäller att  vsv.

Referens: Greenberg M. J. Euclidean and Non-Euclidean Geometries. 3rd Edition, 1993 W.H.Freemann and Co.

Tillbaka till Geometri D