Project in Geometry D,
Autumn Term 2000
Problem
8, Chapter 9:
Prove
the corollary to Theorem 9.6 (p.327)
Theorem 9.6
Let
l and m be two perpendicular lines. Let A be the point of intersection of l and
m. Let T=RlRm (reflection
in l followed by reflection in m). Let B’=T(B).
Then
for every point B not equal to A, A is the midpoint of the straight line BB’.
Remark
T is 180° rotation about A.
Corollary
T is an involution and its
invariant lines are the lines through A.
I Proof of Theorem 9.6:
a)
If B lies on l or m the assertion is clear.
b)
Now assume B doesn’t lie on l or m. Let C be the point from which you
can draw a line through BC such that BC is perpendicular to m. Let C’=T(C).
Then C is on the opposite side of l
from C.
![]() Draw the normal of m
from the point C’. Let B’ be the point such that B’ is on the opposite side of
m from B, and C’B’ is of equal length as BC.
Draw the normal of m
from the point C’. Let B’ be the point such that B’ is on the opposite side of
m from B, and C’B’ is of equal length as BC.
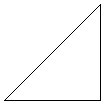 l
l![]() B
B
C’ A
![]()
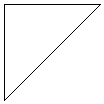 m
m
C
B’
Now ΛBAC≅ΛB’AC’ , AC and AC’ are of equal length and BC and
B’C’ are also of equal length. Therefore B’AC’ and BAC are congruent triangles
and B’AB are collinear.
Thus AB≅AB’ and so A is the midpoint of BB’.
II Proof of the
Corollary
a)
T is an involution.
Definition: An involution is a transformation such that
T‾¹=T.
If B is on l or m then T =Rl or T=Rm, which is an
involution. If B is the point of intersection between l and m (call it A) then
it is invariant under T.
Now let B be a point not equal to A and not
on l or m. Then by Theorem 9.6, there is a point B’=T(B) such that A is the
midpoint of the line BB’. Also, there is a point B’’ such that T(B’)=B’’ and A
is the midpoint of B’B’’.

![]() l
l
B x
![]() m A
m A
B’ x
Now we have two lines BB’ and B’B’’. Since
both lines also go through A, the lines are equal and since AB=AB’=AB’’, it
follows that B=B’’. By our construction T(B)=B’=T‾¹(B’’), so we’ve shown
that T is an involution.
b)
The invariant lines of T are the lines
through A
Definition: A property or
relation is said to be invariant under
a transformation if it still holds after the transformation, f.ex. if a line is
mapped to itself.
(i)
The lines through A
are invariant
Again, if k is a line equal to either l or m
then the action is just Rl or Rm, hence it’s invariant.
Now let k be a line through A not equal to l
or m. In order to show that k is invariant we need to show that any arbitrary
point B on k is mapped to a point on k.
So pick any point B on k, say not equal to A
since if B=A then T(A)=A again.

![]() l k
l k
B x
![]() m A
m A
B’ x
Let B’=T(B), where B’ is a point with the
property that A is the midpoint of BB’. Therefore B’ is on k (otherwise we have
two different lines through A and B, which is not possible) and k is mapped to
itself.
(ii)
No other lines are
invariant
Assume this is not so, i.e. assume there is a
line, say L, such that L is invariant and A is not on L.
Now pick a point P on L. Then T(P)=P’, where
P’ is the point such that A is the midpoint of the straight line, say k, going through
P and P’ (by Theorem 9.6).
Furthermore, since we assumed that L is
invariant, we know that P’ is on L.

![]() l k
l k
 P x L
P x L
![]() m A
m A
P’ x
By construction A is on k but not on L, so k≠L. Both are straight lines
containing P and P’. This is a contradiction, therefore L is not invariant.
The proof of Theorem 9.6 is a restatement of
the proof in ”Euclidean and Non-Euclidean Geometries” (3rd edition),
by Marvin Jay Greenberg.