Term paper

Autumn 2000

In the course Geometry D

by

Stenåke Eriksson

Account for exercise 60, chapter 9 of the book

Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg.

Preface

This term paper about frieze patterns or frieze groups is divided into three parts.

1) What is a frieze pattern or frieze group? Simple explanation necessary for the understanding of the text.

2) There are exactly seven frieze groups, an explanation to why.

3) Solution to problem 60, chapter 9 of the book Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg.

Theorems stated in parts 1 and 2 is given without any proof, since that the main purpose of this text is to solve the problem in part 3.

What is a frieze pattern or frieze group?

A frieze pattern is a 1-dimensional pattern much like a wallpaper border, with some well-defined symmetry.

Example: ...AAAAA... a row with As, a finite motif that is supposed to spread to the left and right infinitely.

In a frieze pattern there is always translation symmetry moving the finite motif. To this translation symmetry there is a corresponding translation vector v always larger then zero but of a finite length that decides the length of the translation. In the pattern there can be other symmetries like reflections rotations or glide according to the following theorem.

THEOREM 3.3 The symmetries of a frieze pattern F

a) The translation symmetries of F are the iterates T_nu of a translation symmetry of least possible magnitude |u|, there n = 0, ±1, ±2...

b) The only 1/n rotation symmetries of F are the identity (n = 1), and 1/2 turns (n = 2).

c) Any line of symmetry of F is either horizontal or vertical.

d) A glide of F must be horizontal.

(For the proofs, see the book: Mathematics for Computer Graphics, p. 42.)

The following abbreviations of the different symmetries are used in this text.

T for translation Ex: T_m for translation along a line m, or T_G for translation part of glide along some line.

H for half-turn Ex: H_A for half-turn around a point A.

R for reflection Ex: R_m for reflection across a line m.

G for glide

A frieze pattern is made up of a collection among four types of symmetries. Among these the glide symmetry can be the one that is most difficult to understand. A glide is a combination of a translation along a line and a reflection in the same line. What so special about the glide is that this combination is supposed to be interpreted as only one symmetry and not a combination of two different symmetries. One way to se a glide is as that symmetry that arise by the footprint then you walk strait forward in the snow.

The following convention is common in connection with frieze and glide.

CONVENTION 3.2 A glide symmetry or glide line of a figure F will normally refer to a composition R_mT_a/2 where a, is a translation vector of F parallel to m, of minimum possible length.

(Used in the book: Mathematics for Computer Graphics, p. 42.)

Now if G = R_mT_a/2 is a glide along a line m, then

G² = (R_mT_a/2)² = R_mT_a/2R_mT_a/2 = T_a

A pure translation along the line m with a length given by the vector a.

Exactly seven frieze groups, an explanation to why.

In a frieze pattern there can be four symmetries:

Translation, Rotation, Reflection and Glide.

The translation symmetry is always a symmetry of a frieze pattern, either as pure translation or as part of a glide.

Possible rotations are: 1 = identity rotation.

2 = half-turn.

Possible reflections in a vertical line: m = if there is a vertical line of symmetry. 1 = for no vertical line of symmetry.

Possible reflections / glide in a horizontal line: m = if there is a horizontal symmetry line. g = horizontal glide line.

1 = neither m nor g.

This can now be combined to give the following combinations.

The first character indicate type of possible rotations, second character possible vertical line symmetry and third character possible horizontal symmetry.

1mm 11m 2mm 21m

1mg 11g 2mg 21g

1m1 111 2m1 211

Of these 12 combinations the over crossed are impossible to made real.

Example 1: 1mm is impossible because explicit reflection both in a vertical and horizontal line give rise to a half-turn, but 1mm say only identity rotations.

Example 2: 2mg are possible because explicit reflection in a vertical line and a horizontal glide line (also a reflection line) give rise to a half-turn.

In Greenberg the seven frieze groups are presented as this.

<T> Translation along an invariant line t.

<T, R_t> Translation along t and a reflection across t.

<T, R_u> Translation along t and a reflection across a perpendicular u to t.

<G> Glide along t.

<T, H_A> Translation and a half-turn about a point A on t.

<T, H_A, R_t>

<G, H_A>

Identification now give the following correspondences...

<T> correspond to 111

<T, R_t> correspond to 11m

<T, R_u> correspond to 1m1

<G> correspond to 11g

<T, H_A> correspond to 211

<T, H_A, R_t> correspond to 2mm

<G, H_A> correspond to 2mg

To identify the type of a frieze pattern the following questions can be asked.

1) Are there vertical mirrors?

2) Is there a horizontal mirror or glide line?

There are 1/2-turn symmetries if and only if the answer to both 1 and 2 is yes.

Example: Frieze pattern ...AAAAA...

There are vertical mirror lines in the middle of each A and in the middle between two A.

Answer YES to question 1 above.

No horizontal mirror line. Answer NO to question 2 above.

This does not give rise to rotation symmetry.

Then the pattern is of type 1m1 and generated by <T, R_u>.

To construct a frieze pattern this is one possible way.

Start with a sub-motif of the pattern with no symmetry.

From the example above, start with a 1/2 A, as this:

Reflection in a vertical mirror line gives a character A as this,

Followed by translation gives this

Repeat this over and over and a frieze pattern arises.

...AAAAA...

Solution to problem 60, chapter 9 of the book Euclidean and Non-Euclidean Geometries by Marvin Jay Greenberg

Problem 9.60

Find the symmetry group off each off the following infinite patterns

(describe the group by generators and relations).

1. ...LLLLL...
2. 

(iii) ...VVVVV...

4. ...NNNNN...
5. 

(vi) ...DDDDD...

(vii) ...HHHHH...

Solution:

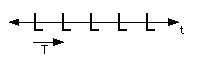i)

No vertical lines of symmetry, no horizontal line of symmetry.

No rotational symmetry.

Only translation of the motif L, according to the figure.

Pattern of type: 111

Pattern generated by: <T>

Only one generator T, every Tⁿ (n integer) is distinct.

There are no relations for this group.

ii)

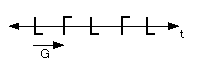No vertical lines of symmetry, horizontal line of symmetry in the form of glide along t.

No rotational symmetry.

Pattern of type: 11g

Pattern generated by: <G>

Relations:

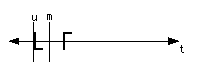Let G = R_tT_G there T_G = R_mR_u u and m perpendicular mirror lines to t.

T_G translation of glide

then

G = R_tT_G = R_tR_mR_u = R_uR_mR_t = T_GR_t since u and m perpendicular to t.

and

G² = (R_tT_G)²=R_tT_GR_tT_G = T_GR_tR_tT_G = T_GT_G = T pure translation

G² = T

iii)

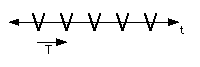Vertical lines of symmetry through every V, and in the middle between consecutive V.

No horizontal line of symmetry.

No rotational symmetry.

Pattern of type: 1m1

Pattern generated by: <T, R_u>

Relations: Case 1

Let T = R_mR_u then

TR_u = R_mR_uR_u = R_m and

R_uT = R_uR_mR_u and

TR_{u ¹} R_uT u and m parallel and reflections in parallel lines do not commute

Case 2: u and m change place

Let T = R_uR_m then

TR_u = R_uR_mR_u and

R_uT = R_uR_uR_m = R_m and finally

TR_u ¹ R_uT

iv)

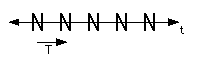No vertical lines of symmetry, no horizontal line of symmetry.

Rotational symmetry in the middle of every N and between consecutive N.

Pattern of type: 211

Pattern generated by: <T, H_A>

Relations: Case 1

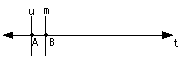Let T = R_mR_u and H_A = R_tR_u

TH_A = R_mR_uR_tR_u = R_mR_uR_uR_t = R_mR_t = H_B m and t perpendicular

H_AT = R_tR_uR_mR_u = R_uR_mR_tR_u = T^-1H_A

and

TH_A = H_B

H_AT = T^-1H_A

Case 2: Let A and B change place.

Let T = R_mR_u and H_A = R_tR_m

TH_A = R_mR_uR_tR_m = R_tR_mR_uR_m = H_A T^-1 m and t perpendicular

H_AT = R_tR_mR_mR_u = R_tR_u = H_B

and finally

TH_A = H_AT^-1

H_AT = H_B

v)

Vertical lines of symmetry, horizontal line of symmetry in the form of glide along t, gives

rotational symmetry in the middle between consecutive characters.

Pattern of type: 2mg

Pattern generated by: <G, H_A>

Relations:

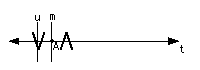Let G = R_tT_G , T_G = R_mR_u then G = R_tR_mR_u and H_A = R_tR_m

GH_A = R_tR_mR_uRtR_m = R_tR_tR_mR_uR_m = R_mR_uR_m u, m parallel mirror lines

H_AG = R_tR_mR_tR_mRu = R_tR_tR_mR_mR_u = R_u

and

GH_A ¹ H_AG

vi)

No vertical lines of symmetry, horizontal line of symmetry.

No rotational symmetry.

Pattern of type: 11m

Pattern generated by: <T, R_t>

Relations:

Let T = R_mR_u u and m perpendicular mirror lines to t.

TR_t = R_mR_uR_t = R_tR_mR_u = R_tT

and

TR_t = R_tT generators commute

vii)

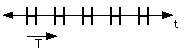Vertical lines of symmetry, horizontal line of symmetry.

Rotational symmetry in the middle of every H and between consecutive H.

Pattern of type: 2mm

Pattern generated by : <T, H_A, R_t>

Relations:

Let T =R_mR_u and H_A = R_tR_u

TH_AR_t = R_mR_uR_tR_uR_t = R_m

TR_tH_A = R_mR_uR_tR_tR_u = R_m

H_ATR_t = R_tR_uR_mR_uR_t = R_uR_tR_mR_tR_u = R_uR_tR_tR_mR_u = R_uR_mR_u

H_AR_tT = R_tR_uR_tR_mR_u = R_uR_mR_u

R_tH_AT = R_tR_tR_uR_mR_u =R_uR_mR_u

R_tTH_A = R_tR_mR_uR_tR_u = R_tR_mR_tR_uR_u = R_tR_mR_t = R_tR_tR_m = R_m

and the result is

TH_AR_t = TR_tH_A = R_tTH_A

H_ATR_t = H_AR_tT = R_tH_AT

Any case there mirror lines or points A and B change place give the same result

References

Marvin Jay Greenberg (1993) Euclidean and Non-Euclidean Geometries

W.H. Freeman and Company

S.G Hoggar (1994) Mathematics for Computer Graphics

CAMBRIDGE UNIVERSITY PRESS

Ralph P. Grimaldi (1994) DISCRETE AND COMBINATORIAL MATHEMATICS 3.ed

Addison-Wesley Publishing Company