Svensk löste matematisk utmaning
Kaosproblem. Lorenzattraktorn är verkligen kaotisk.Av Jesper Sollerman
Det handlar alltså om kaos. Ett begrepp som närmast revolutionerade naturvetenskapen under 1970- och 1980-talen. Alltsedan Newtons sextonhundratal hade fysikerna sett på världen som ett gigantiskt urverk. När klockan väl var uppdragen gick den enligt klara och förutsägbara lagar. Den franske vetenskapsmannen Laplace menade att om man kunde veta vad alla universums partiklar har för läge och hastighet just nu, skulle man kunna återskapa det förflutna och förutsäga universums hela framtid. Allting var välordnat och förutbestämt, enligt den tidens sätt att se på saken.
Både relativitetsteorin och kvantmekaniken, de två stora revolutionerna inom nittonhundratalets fysik, ruckade en smula på Newtons världsbild. Men dessa teorier handlar om hastigheter nära ljushastigheten, tyngdkraftfält vid svarta hål och om mikrokosmos i atomernas värld. I vardagslivet verkade Newtons gamla hederliga mekanik i alla fall fungera.
Astronomerna kan förutsäga solförmörkelser med sådan precision att man nästan glömmer att det rör sig om prognoser. Med vädret förhåller det sig lite annorlunda. Som alla vet efter årets sommar är det mycket svårt att förutsäga vädret med någon större säkerhet.
Meteorologerna trodde dock länge att med bättre datorer och noggrannare mätvärden från vädersatelliterna skulle det i princip vara möjligt med exakta väderprognoser också för långa tidsperioder. Det visade sig vara fel.
Edward Lorenz var en matematiskt lagd meteorolog som på sextiotalet använde sin nyanskaffade dator för att göra en enkel vädermodell. Han begränsade problemet till tre enkla differentialekvationer, ett till synes elementärt problem. Men Lorenz upptäckte att utfallen i hans beräkningar var oerhört känsliga för vilka värden han matade in i datorn. Om han bara ändrade en smula i decimalerna betedde sig hans vädermodell fullständigt annorlunda. Till en början trodde Lorenz att det var hans dator som krånglade, kanske hade ett gammalt rör gått sönder. Sedan insåg han att han hade upptäckt någonting viktigt och grundläggande.
Den enorma känsligheten för startvärden som Lorenz ekvationer uppvisade kallade han för fjärilseffekten. Mycket små förändringar kan få mycket stora konsekvenser också i ganska enkla system. En fjärils fladdrande i Brasilien skulle kunna orsaka en framtida orkan i Texas.
Detta var ett hårt slag för den newtonska världsbilden. Inte ens i princip kan vi bestämma alla mätvärden hur exakt som helst och därför kan vi för dessa kaotiska system inte heller göra några meningsfulla förutsägelser för längre tidsperioder. Oavsett vilken upplösning meteorologernas satelliter har och hur snabba deras superdatorer är kan de inte förutsäga i november om det blir snö på julafton.
Det existerar kaotiska system som är för alltid oförutsägbara.
Lösningarna till Lorenz tre ekvationer visade en oanad komplexitet och banade vägen för den moderna kaosforskningen. Men ur kaos kommer också ordning.
Om en luftmolekyls rörelse bestäms av Lorenz ekvationer och man ritar upp hur dess läge förändras med tiden får man en besynnerlig figur kallad Lorenzattraktorn.
Banan blir en fjärilsliknande dubbelspiral som aldrig skär sig själv. Geometrin hos denna figur kallas fraktal och molekylens rörelse är kaotisk. Banan sluts aldrig men begränsas ändå, den lämnar aldrig den ordnade fjärilsliknande figuren. Rörelsen för den individuella luftmolekylen är alltså helt omöjlig att förutsäga, man kan aldrig veta om luftmolekylen kommer att befinna sig i den högra eller vänstra spiralen om en liten stund. Men den kaotiska rörelsen bygger upp en vacker och välordnad struktur.
- Man kan kanske likna det vid en tromb, säger Warwick Tucker.
Trots att luftmolekylerna i en tromb yr omkring helt slumpmässigt ser alltid en tromb ungefär likadan ut, som en lång strut. Den överliggande strukturen är alltså ganska ordnad, trots att den är uppbygd av partiklar som rör sig kaotiskt. Lorenzattraktorn är ju bara en matematisk konstruktion, men den visar på samma sätt hur en kaotisk rörelse ändå följer vissa spelregler och kan bygga upp en ordning.
Åtminstone är detta vad kaosforskarna har antagit sedan Lorenz upptäckt; att lösningarna till Lorenz ekvationer är kaotiska. Lorenzattraktorn har varit ett av kaosforskningens flaggskepp. Men rent matematiskt har det varit oerhört svårt att bevisa att ekvationerna verkligen är kaotiska. Många och långa datorkörningar har ritat upp den numera välkända fjärilsfiguren utan att någon någonsin har sett banan korsa sig själv. Men kanske har man helt enkelt inte räknat tillräckligt länge. Man kan ju tänka sig att banan faktiskt är periodisk, men med en mycket lång period.
Problemet påminner en smula om ett av de mest kända matematiska problemen som finns, Fermats sista sats. Denna sats formulerades av sextonhundratalsmatematikern Fermat och säger, enkelt uttryckt, att Pythagoras sats endast gäller för exponenten två.
Fermat själv ansåg sig ha ett bra bevis för det hela men skrev aldrig ner detta eftersom, som han uttryckte det i sina anteckningar, "marginalen är för smal".
Med en dator är det en barnlek att visa att Fermats sats gäller upp till väldigt stora tal. Men det duger inte för en matematiker. Ett matematiskt bevis måste en gång för alla visa att satsen gäller för alla tal som överhuvudtaget existerar. Det måste vara allmängiltigt och vattentätt.
Utmaningen att hitta ett strikt bevis för Fermats sista sats gäckade matematikerna i över 300 år. Det ansågs som en stor vetenskaplig sensation när den engelske matematikern Andrew Wiles 1995 lade fram sitt 129 sidor långa bevis för satsens riktighet.
Lorenzattraktorns egenskaper har också gäckat många matematiker. Då den berömde matematikern Steve Smale, en av kaosforskningens förgrundsfigurer, ombads formulera de viktigaste matematiska problemen inför nästa århundrade i tidskriften "The Matematical Intelligencer", listade han Lorenzattraktorn som ett av 18 problem.
Nu är det alltså löst.
Warwick Tucker är 27 år gammal och kom till Sverige från Australien som femåring. Han bosatte sig i Uppsala och är i dag verksam som doktorand på den matematiska institutionen vid universitetet. Mycket av hans forskning sker i samarbete med matematiker på KTH i Stockholm.
- Det var min handledare som tipsade mig om problemet med Lorenzattraktorn. De flesta matematiska avhandlingarna innehåller ett flertal mindre problem, men jag har valt att satsa allt på ett kort , berättar Warwick Tucker.
Han har arbetat med Lorenzekvationerna i över fyra år.
Warwick Tuckers bevis för att Lorenzattraktorn är kaotisk visar att fjärilsfigurens banor aldrig kommer att korsas oavsett hur länge man låter sin dator räkna. Banan kommer att i stället nästlas allt tätare i sin fraktala geometri, men den kommer aldrig slutas. Beviset är tämligen okonventionellt, det drygt 100 sidor långa beviset inkluderar nämligen ett datorprogram. Det är ganska ovanligt i den matematiska världen, där det mesta brukar bevisas med papper och penna.
- Ett sådant här bevis hade inte varit möjligt för tio år sedan. Med dagens snabba datorer tar beräkningarna fortfarande nästan ett dygn, förklarar Warwick Tucker.
Den tekniska utvecklingen gör att datorer blir allt intressantare för matematisk bevisföring. Det är lika matematisk rigoröst som de traditionella bevisen, försäkrar Warwick Tucker.
Den 24 september ska han presentera beviset vid sin disputation. Därefter flyttar han till Brasilien där han ska studera vilka praktiska tilllämpningar hans nya upptäckt kan användas till.
- Det här handlar ju fortfarande om matematisk grundforskning, betonar Warwick Tucker. Men i princip kan metoden användas för att ge riktiga feluppskattningar för många sorters system.
Tids nog kan kanske den nya metoden användas för att få pålitligare väderprognoser. Med årets sommar i färskt minne verkar ju detta vara nog så angelägen forskning.
Jesper Sollerman är doktorand i astronomi
och vetenskapsjournalist

Warwick Tucker har bevisat kaos.
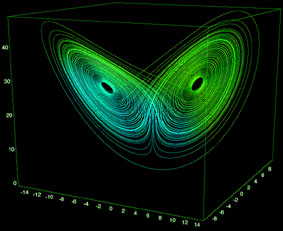
Beviset i form av en dataritad
fjäril.