Listen
Master/PhD Projects
Quasicrystals, Schrödinger operators and hyperbolic dynamics
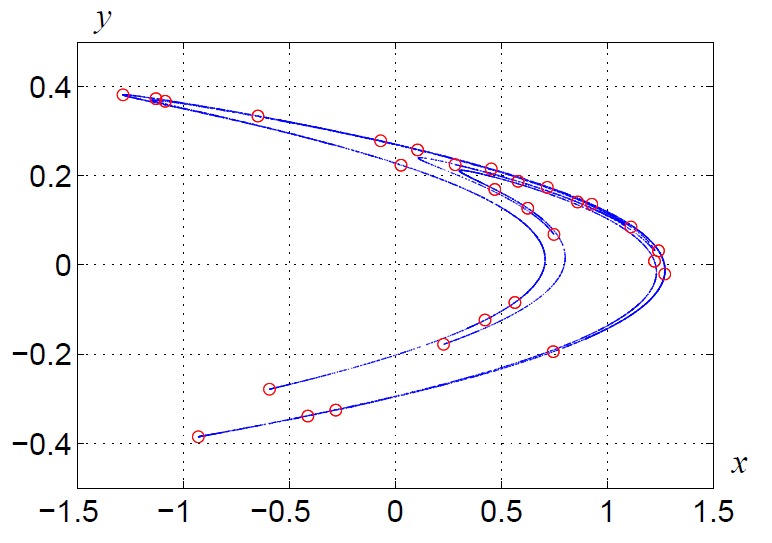
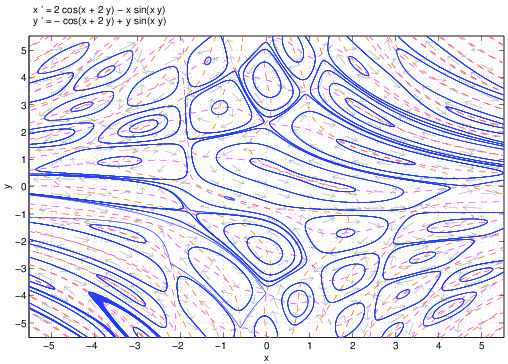
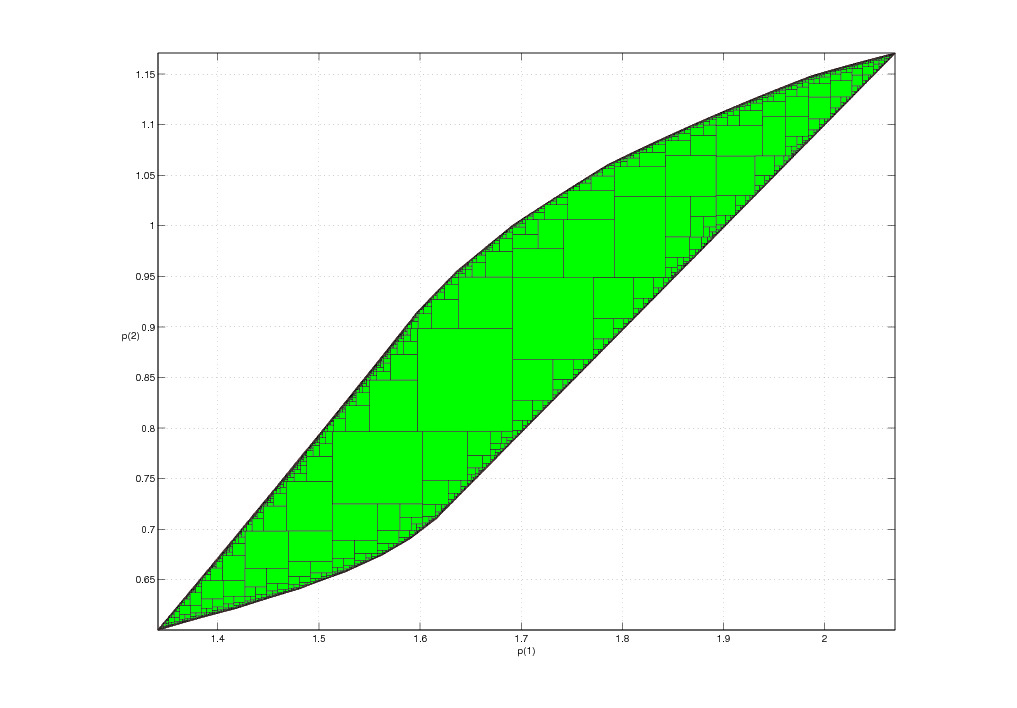
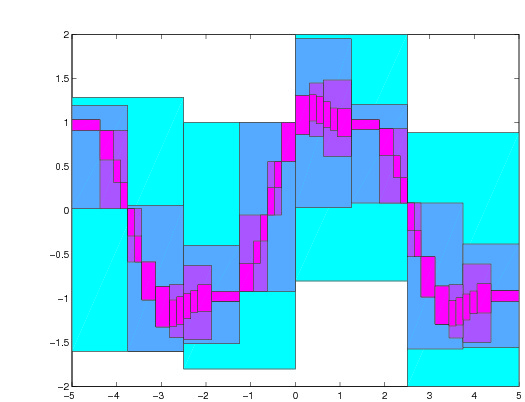
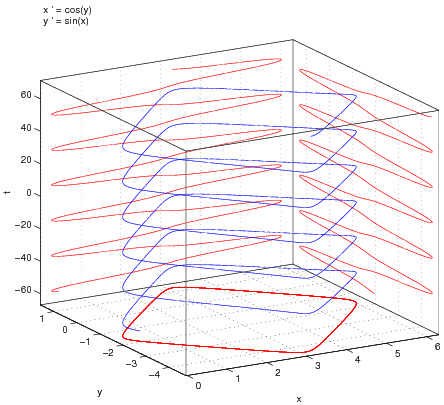
The connections between quasicrystals, Schrödinger operators and hyperbolic dynamics will be studied. More concretely, it will be studied the hyperbolicity structure of the trace map associated to the Fibonacci Hamiltonian Schrödinger operator. This study will be performed with the help of numerical simulations and/or validated numerics. The goal is setting up the numerical tools necessary for proving a conjecture by Gorodeski and Damanik.
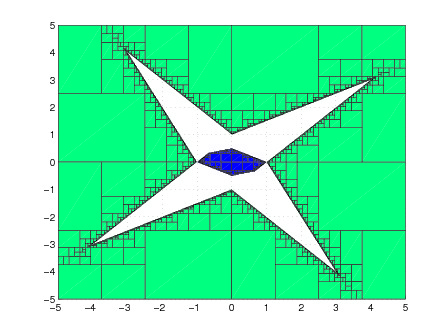
The ability of coding in C or FORTRAN will be desirable. This thesis will provide to the student profound knowledge in dynamical systems and its comptuational part. For more information, contact Jordi-Lluís Figueras.Numerical study of periodic orbits in polygonal billiards
The goal of this thesis is performing a numerical study of a long standing conjecture by Katok about the existence of periodic orbits in polygonal billiard. More concretely, we propose studying how to construct periodic orbits in triangular billiards. A posteriori, these orbits will be validated by means of rigorous numerics.
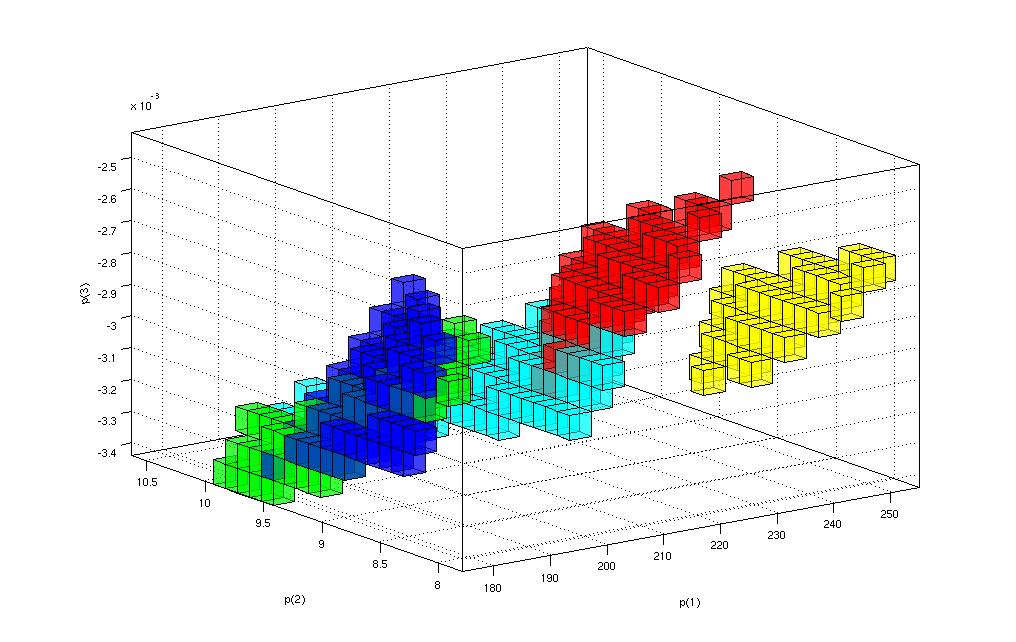
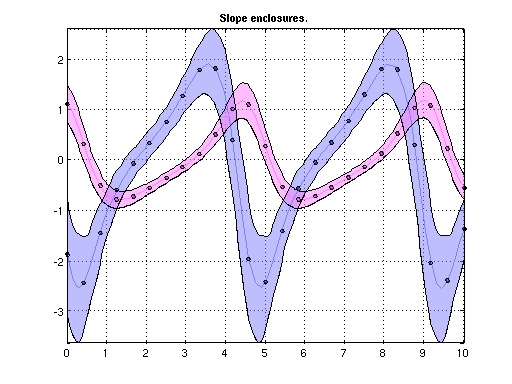
The ability of coding in C or FORTRAN will be desirable. This thesis will provide to the student profound knowledge in dynamical systems and its comptuational part. For more information, contact Jordi-Lluís Figueras.Parameter estimation for dynamical systems
The goal of this project is to devise mathematical and numerical methods for finding the parameters of a dynamical system that make it match observed data. In the simplest scenario, the dynamical system is a map, but differential equations can also be studied. The numerical part of this project will be carried out on the GPU architecture, utilizing its ability for massively parallel computations. The mathematical part will involve set-valued constraint propagation.
The ability to program in C or C++ is desirable. The thesis will provide a deep knowledge in parameter estimation and GPU-computing. For more information, contact Warwick Tucker.Relative equilibria for the n-body problem
The goal of this project is to find the number of special configurations, known as relative equilibria, in the classical n-body problem from celestial mechanics. This involves developing special solvers for the problem, and to study the bifurcations taking place as the masses of the planets vary. This project can be mostly theoretical, or combined with a strong numerical component. In the latter case, validated numerics will be employed to ensure the mathematical correctness of the numerical results.
A basic knowledge of dynamical systems is desirable, as is the ability to program in C or C++. The thesis will provide a deep knowledge of bifurcation theory, dynamical systems, and validated numerics. For more information, contact Warwick Tucker.Renormalization and strange attractors in two-dimensional maps
The goal of the project is to study "strange attractors" in two-dimensional dissipative maps which are "far" from being one-dimensional. Existence of such objects in very small perturbations of one-dimensional quadratic maps consitutes the celebrated result of L. Carleson and M. Benedicks. Recently developed renormalization techniques for dissipative two-dimensional maps allow to consider perturbations which are not too small. How large can such perturbations be, what is the geometry of the starnge attractors for large perturbations, how often such strange attractors are found in a typical family of maps - these are some of the issues that will be addressed during the project.
The project contains both a theoretical and a computational component, which can be studied together or separately. A basic knowledge of dynamical systems and programming skills are desirable. For more information, contact Denis Gaidashev.Geometry of Siegel disks
The goal of the project is to study the geometry of Siegel disks - fractal subsets of the complex plain that appear as linearization domains for certain maps of the complex plain. Such domains exhibit self-similarity and small-scale fine structure. Many geometrical features of these objects can be (and have been) understood with the help of techniques from the renormalization theory and conformal dynamics. A number of interesting questions remain, such as, how similar are Siegel disk of two "similar" analytic maps (i.e. maps, whose linearizations coincide).
This project is mostly theoretical, but can involve numerical simulations and computer-assisted proofs. A basic knowledge of complex dynamics and some programming skills are desirable. For more information, contact Denis Gaidashev.